Portal:Mathematics

Abacus, a ancient hand-operated calculating.
Portrait of Emmy Noether, around 1900.
Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

Image 1

Portrait by Jakob Emanuel Handmann, 1753

Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] , Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.

Euler is credited for popularizing the Greek letter π {\displaystyle \pi } (lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation f ( x ) {\displaystyle f(x)} for the value of a function, the letter i {\displaystyle i} to express the imaginary unit − 1 {\displaystyle {\sqrt {-1}}} , the Greek letter Σ {\displaystyle \Sigma } (capital sigma) to express summations, the Greek letter Δ {\displaystyle \Delta } (capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant e {\displaystyle e} , the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...)
Image 2

Archimedes Thoughtful by Fetti (1620)

Archimedes of Syracuse (/ˌɑːrkɪˈmiːdiːz/ AR-kim-EE-deez; c. 287 – c. 212 BC) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is considered one of the leading scientists in classical antiquity. Regarded as the greatest mathematician of ancient history, and one of the greatest of all time, Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.

Archimedes' other mathematical achievements include deriving an approximation of pi ( $π$ ), defining and investigating the Archimedean spiral, and devising a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, working on statics and hydrostatics. Archimedes' achievements in this area include a proof of the law of the lever, the widespread use of the concept of center of gravity, and the enunciation of the law of buoyancy known as Archimedes' principle. In astronomy, he made measurements of the apparent diameter of the Sun and the size of the universe. He is also credited with designing innovative machines, such as his screw pump, compound pulleys, and defensive war machines to protect his native Syracuse from invasion. (Full article...)
Image 3

One of Molyneux's celestial globes, which is displayed in Middle Temple Library – from the frontispiece of the Hakluyt Society's 1889 reprint of A Learned Treatise of Globes, both Cœlestiall and Terrestriall, one of the English editions of Robert Hues' Latin work Tractatus de Globis (1594)

Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.

Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...)
Image 4

Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.

Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)
Image 5
The weighing pans of this balance scale contain zero objects, divided into two equal groups.

In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if $y$ is even then $y + x$ has the same parity as $x$ —indeed, $0 + x$ and $x$ always have the same parity.

Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
Image 6

A stamp of Zhang Heng issued by China Post in 1955

Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Eastern Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.

Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...)
Image 7

Portrait by August Köhler, c. 1910, after 1627 original

Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.

Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
Image 8
In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.

Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...)
Image 9

The title page of a 1634 version of Hues' Tractatus de globis in the collection of the Biblioteca Nacional de Portugal

Robert Hues (1553 – 24 May 1632) was an English mathematician and geographer. He attended St. Mary Hall at Oxford, and graduated in 1578. Hues became interested in geography and mathematics, and studied navigation at a school set up by Walter Raleigh. During a trip to Newfoundland, he made observations which caused him to doubt the accepted published values for variations of the compass. Between 1586 and 1588, Hues travelled with Thomas Cavendish on a circumnavigation of the globe, performing astronomical observations and taking the latitudes of places they visited. Beginning in August 1591, Hues and Cavendish again set out on another circumnavigation of the globe. During the voyage, Hues made astronomical observations in the South Atlantic, and continued his observations of the variation of the compass at various latitudes and at the Equator. Cavendish died on the journey in 1592, and Hues returned to England the following year.

In 1594, Hues published his discoveries in the Latin work Tractatus de globis et eorum usu (Treatise on Globes and Their Use) which was written to explain the use of the terrestrial and celestial globes that had been made and published by Emery Molyneux in late 1592 or early 1593, and to encourage English sailors to use practical astronomical navigation. Hues' work subsequently went into at least 12 other printings in Dutch, English, French and Latin. (Full article...)
Image 10

Noether c. 1900–1910

Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She also proved Noether's first and second theorems, which are fundamental in mathematical physics. Noether was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.

Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
Image 11

Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.

In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history". In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics". (Full article...)
Image 12
Plots of logarithm functions, with three commonly used bases. The special points $log b b = 1$ are indicated by dotted lines, and all curves intersect in $log b 1 = 0$ .

In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of $1000$ to base $10$ is $3$ , because $1000$ is $10$ to the $3$ rd power: $1000 = 10 3 = 10 \times 10 \times 10$ . More generally, if $x = b y$ , then $y$ is the logarithm of $x$ to base $b$ , written $log b x$ , so $log 10 1000 = 3$ . As a single-variable function, the logarithm to base $b$ is the inverse of exponentiation with base $b$ .

The logarithm base $10$ is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number $e \approx 2.718$ as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base $2$ and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written $log x$ . (Full article...)
Image 13
The first 15,000 partial sums of 0 + 1 − 2 + 3 − 4 + ... The graph is situated with positive integers to the right and negative integers to the left.

In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as
$\sum _{n=1}^{m}n(-1)^{n-1}.$

The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:
$1-2+3-4+\cdots ={\frac {1}{4}}.$ (Full article...)
Image 14

Elementary algebra studies which values solve equations formed using arithmetical operations.

Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.

Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
Image 15
The number π (/paɪ/ ; spelled out as "pi") is a mathematical constant, approximately equal to 3.14159, that is the ratio of a circle's circumference to its diameter. It appears in many formulae across mathematics and physics, and some of these formulae are commonly used for defining π, to avoid relying on the definition of the length of a curve.

The number π is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as 22 7 {\displaystyle {\tfrac {22}{7}}} are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an algebraic equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. (Full article...)

Good articles

Image 1
Advanced Placement (AP) Statistics (also known as AP Stats) is a college-level high school statistics course offered in the United States through the College Board's Advanced Placement program. This course is equivalent to a one semester, non-calculus-based introductory college statistics course and is normally offered to sophomores, juniors and seniors in high school.

One of the College Board's more recent additions, the AP Statistics exam was first administered in May 1996 to supplement the AP program's math offerings, which had previously consisted of only AP Calculus AB and BC. In the United States, enrollment in AP Statistics classes has increased at a higher rate than in any other AP class. (Full article...)
Image 2
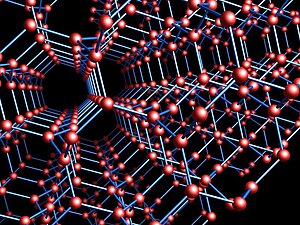
The Laves graph

In geometry and crystallography, the Laves graph is an infinite and highly symmetric system of points and line segments in three-dimensional Euclidean space, forming a periodic graph. Three equal-length segments meet at 120° angles at each point, and all cycles use ten or more segments. It is the shortest possible triply periodic graph, relative to the volume of its fundamental domain. One arrangement of the Laves graph uses one out of every eight of the points in the integer lattice as its points, and connects all pairs of these points that are nearest neighbors, at distance ${\sqrt {2}}$ . It can also be defined, divorced from its geometry, as an abstract undirected graph, a covering graph of the complete graph on four vertices.
H. S. M. Coxeter (1955) named this graph after Fritz Laves, who first wrote about it as a crystal structure in 1932. It has also been called the K₄ crystal, (10,3)-a network, diamond twin, triamond, and the srs net. The regions of space nearest each vertex of the graph are congruent 17-sided polyhedra that tile space. Its edges lie on diagonals of the regular skew polyhedron, a surface with six squares meeting at each integer point of space. (Full article...)
Image 3
In graph theory, a cop-win graph is an undirected graph on which the pursuer (cop) can always win a pursuit–evasion game against a robber, with the players taking alternating turns in which they can choose to move along an edge of a graph or stay put, until the cop lands on the robber's vertex. Finite cop-win graphs are also called dismantlable graphs or constructible graphs, because they can be dismantled by repeatedly removing a dominated vertex (one whose closed neighborhood is a subset of another vertex's neighborhood) or constructed by repeatedly adding such a vertex. The cop-win graphs can be recognized in polynomial time by a greedy algorithm that constructs a dismantling order. They include the chordal graphs, and the graphs that contain a universal vertex. (Full article...)
Image 4
Hypatia (born c. 350–370 - March 415 AD) was a Neoplatonist philosopher, astronomer, and mathematician who lived in Alexandria, Egypt, then part of the Eastern Roman Empire. She was a prominent thinker in Alexandria where she taught philosophy and astronomy. Although preceded by Pandrosion, another Alexandrian female mathematician, she is the first female mathematician whose life is reasonably well recorded. Hypatia was renowned in her own lifetime as a great teacher and a wise counselor. She wrote a commentary on Diophantus's thirteen-volume Arithmetica, which may survive in part, having been interpolated into Diophantus's original text, and another commentary on Apollonius of Perga's treatise on conic sections, which has not survived. Many modern scholars also believe that Hypatia may have edited the surviving text of Ptolemy's Almagest, based on the title of her father Theon's commentary on Book III of the Almagest.

Hypatia constructed astrolabes and hydrometers, but did not invent either of these, which were both in use long before she was born. She was tolerant toward Christians and taught many Christian students, including Synesius, the future bishop of Ptolemais. Ancient sources record that Hypatia was widely beloved by pagans and Christians alike and that she established great influence with the political elite in Alexandria. Toward the end of her life, Hypatia advised Orestes, the Roman prefect of Alexandria, who was in the midst of a political feud with Cyril, the bishop of Alexandria. Rumors spread accusing her of preventing Orestes from reconciling with Cyril and, in March 415 AD, she was murdered by a mob of Christians led by a lector named Peter. (Full article...)
Image 5
Stars is a wood engraving print created by the Dutch artist M. C. Escher in 1948, depicting two chameleons in a polyhedral cage floating through space.

The compound of three octahedra used for the central cage in Stars had been studied before in mathematics, and Escher likely learned of it from the book Vielecke und Vielflache by Max Brückner. Escher used similar compound polyhedral forms in several other works, including Crystal (1947), Study for Stars (1948), Double Planetoid (1949), and Waterfall (1961). (Full article...)
Image 6
The boundary of a Reuleaux triangle is a constant width curve based on an equilateral triangle. All points on a side are equidistant from the opposite vertex.

A Reuleaux triangle [ʁœlo] is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because its width is constant, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"

They are named after Franz Reuleaux, a 19th-century German engineer who pioneered the study of machines for translating one type of motion into another, and who used Reuleaux triangles in his designs. However, these shapes were known before his time, for instance by the designers of Gothic church windows, by Leonardo da Vinci, who used it for a map projection, and by Leonhard Euler in his study of constant-width shapes. Other applications of the Reuleaux triangle include giving the shape to guitar picks, fire hydrant nuts, pencils, and drill bits for drilling filleted square holes, as well as in graphic design in the shapes of some signs and corporate logos. (Full article...)
Image 7
In this example, the alternating sum of angles (clockwise from the bottom) is 90° − 45° + 22.5° − 22.5° + 45° − 90° + 22.5° − 22.5° = 0°. Since it adds to zero, the crease pattern may be flat-folded.

Kawasaki's theorem or Kawasaki–Justin theorem is a theorem in the mathematics of paper folding that describes the crease patterns with a single vertex that may be folded to form a flat figure. It states that the pattern is flat-foldable if and only if alternatingly adding and subtracting the angles of consecutive folds around the vertex gives an alternating sum of zero.
Crease patterns with more than one vertex do not obey such a simple criterion, and are NP-hard to fold.

The theorem is named after one of its discoverers, Toshikazu Kawasaki. However, several others also contributed to its discovery, and it is sometimes called the Kawasaki–Justin theorem or Husimi's theorem after other contributors, Jacques Justin and Kôdi Husimi. (Full article...)
Image 8
A double bubble. Note that the surface separating the small lower bubble from the large bubble bulges into the large bubble.

In the mathematical theory of minimal surfaces, the double bubble theorem states that the shape that encloses and separates two given volumes and has the minimum possible surface area is a standard double bubble: three spherical surfaces meeting at angles of 120° on a common circle. The double bubble theorem was formulated and thought to be true in the 19th century, and became a "serious focus of research" by 1989, but was not proven until 2002.

The proof combines multiple ingredients. Compactness of rectifiable currents (a generalized definition of surfaces) shows that a solution exists. A symmetry argument proves that the solution must be a surface of revolution, and it can be further restricted to having a bounded number of smooth pieces. Jean Taylor's proof of Plateau's laws describes how these pieces must be shaped and connected to each other, and a final case analysis shows that, among surfaces of revolution connected in this way, only the standard double bubble has locally-minimal area. (Full article...)
Image 9
The graph of the 3-3 duoprism (the line graph of $K_{3,3}$ ) is perfect. Here it is colored with three colors, with one of its 3-vertex maximum cliques highlighted.

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

The perfect graphs include many important families of graphs and serve to unify results relating colorings and cliques in those families. For instance, in all perfect graphs, the graph coloring problem, maximum clique problem, and maximum independent set problem can all be solved in polynomial time, despite their greater complexity for non-perfect graphs. In addition, several important minimax theorems in combinatorics, including Dilworth's theorem and Mirsky's theorem on partially ordered sets, Kőnig's theorem on matchings, and the Erdős–Szekeres theorem on monotonic sequences, can be expressed in terms of the perfection of certain associated graphs. (Full article...)
Image 10

Escher in 1971

Maurits Cornelis Escher (/ˈɛʃər/; Dutch: [ˈmʌurɪts kɔrˈneːlɪs ˈɛɕər]; 17 June 1898 – 27 March 1972) was a Dutch graphic artist who made woodcuts, lithographs, and mezzotints, many of which were inspired by mathematics.
Despite wide popular interest, for most of his life Escher was neglected in the art world, even in his native Netherlands. He was 70 before a retrospective exhibition was held. In the late twentieth century, he became more widely appreciated, and in the twenty-first century he has been celebrated in exhibitions around the world.

His work features mathematical objects and operations including impossible objects, explorations of infinity, reflection, symmetry, perspective, truncated and stellated polyhedra, hyperbolic geometry, and tessellations. Although Escher believed he had no mathematical ability, he interacted with the mathematicians George Pólya, Roger Penrose, and Donald Coxeter, and the crystallographer Friedrich Haag, and conducted his own research into tessellation. (Full article...)
Image 11
Schwarz lantern on display in the German Museum of Technology, Berlin

In mathematics, the Schwarz lantern is a polyhedral approximation to a cylinder, used as a pathological example of the difficulty of defining the area of a smooth (curved) surface as the limit of the areas of polyhedra. It is formed by stacked rings of isosceles triangles, arranged within each ring in the same pattern as an antiprism. The resulting shape can be folded from paper, and is named after mathematician Hermann Schwarz and for its resemblance to a cylindrical paper lantern. It is also known as Schwarz's boot, Schwarz's polyhedron, or the Chinese lantern.

As Schwarz showed, for the surface area of a polyhedron to converge to the surface area of a curved surface, it is not sufficient to simply increase the number of rings and the number of isosceles triangles per ring. Depending on the relation of the number of rings to the number of triangles per ring, the area of the lantern can converge to the area of the cylinder, to a limit arbitrarily larger than the area of the cylinder, or to infinity—in other words, the area can diverge. The Schwarz lantern demonstrates that sampling a curved surface by close-together points and connecting them by small triangles is inadequate to ensure an accurate approximation of area, in contrast to the accurate approximation of arc length by inscribed polygonal chains. (Full article...)
Image 12

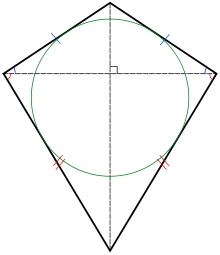
A kite, showing its pairs of equal-length sides and its inscribed circle.

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombi, with two diagonal axes of symmetry; and the squares, which are also special cases of both right kites and rhombi. (Full article...)

Did you know

... that despite published scholarship to the contrary, Andrew Planta neither received a doctorate nor taught mathematics at Erlangen?
... that subgroup distortion theory, introduced by Misha Gromov in 1993, can help encode text?
... that multiple mathematics competitions have made use of Sophie Germain's identity?
... that Green Day's "Wake Me Up When September Ends" became closely associated with the aftermath of Hurricane Katrina?
... that the British National Hospital Service Reserve trained volunteers to carry out first aid in the aftermath of a nuclear or chemical attack?
... that after Archimedes first defined convex curves, mathematicians lost interest in their analysis until the 19th century, more than two millennia later?
... that Latvian-Soviet artist Karlis Johansons exhibited a skeletal tensegrity form of the Schönhardt polyhedron seven years before Erich Schönhardt's 1928 paper on its mathematics?
... that people in Madagascar perform algebra on tree seeds in order to tell the future?

Did you know...

...work in artificial intelligence makes use of swarm intelligence, which has foundations in the behavioral examples found in nature of ants, birds, bees, and fish among others?
...that statistical properties dictated by Benford's Law are used in auditing of financial accounts as one means of detecting fraud?
...that modular arithmetic has application in at least ten different fields of study, including the arts, computer science, and chemistry in addition to mathematics?
... that according to Kawasaki's theorem, an origami crease pattern with one vertex may be folded flat if and only if the sum of every other angle between consecutive creases is 180º?
... that, in the Rule 90 cellular automaton, any finite pattern eventually fills the whole array of cells with copies of itself?
... that, while the criss-cross algorithm visits all eight corners of the Klee–Minty cube when started at a worst corner, it visits only three more corners on average when started at a random corner?
...that in senary, all prime numbers other than 2 and 3 end in 1 or a 5?

More did you know facts

Showing 7 items out of 75

Featured pictures

$Image 1Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)$

Image 1Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 2Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 3Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 4Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 5Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 6Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 7Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 8Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 9Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 10Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 11Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 12Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 13Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 14Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 15Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 16Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 17Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 18Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 19Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 20Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 21Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 22Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 23Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 24Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 25Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 26Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 27Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 28Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 29Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 30Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
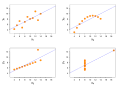
Image 31Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 32Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 33Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 34Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals